LeetCode--Container With Most Water

发表于 | 分类于 |

题目描述：

Given n non-negative integers a1, a2, …, an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

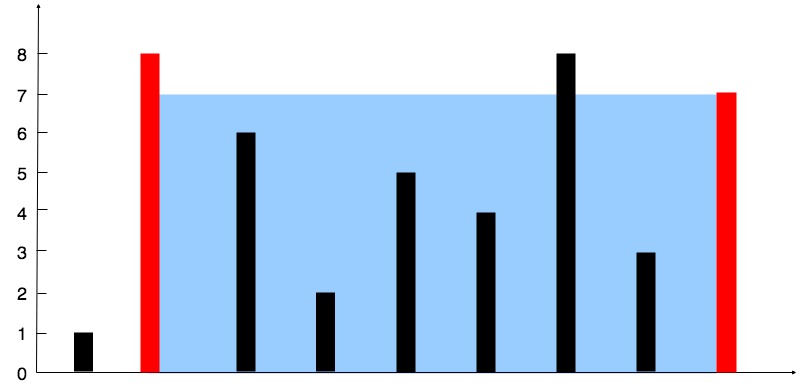
Container With Most Water

The above vertical lines are represented by array [1,8,6,2,5,4,8,3,7]. In this case, the max area of water (blue section) the container can contain is 49.

样例：

1
2
Input: [1,8,6,2,5,4,8,3,7]
Output: 49

题意：

给出 n 个非负整数 $a_1, a_2, …, a_n$，其中每个表示在第 $i$ 处高度为 $a_i$，然后如上图一样，往里面倒水，能够存储的最多的水是多少？

思路：

就由于 $a_i$ 和 $a_j(i < j)$ 组成的面积为：$s(i, j) = min(a_i, a_j) * (j - i)$；

所以对于任何 $s(i’ >= i, j’ <= j) >= s(i, j)$，由于 $j - i <= j’ - i’$，必然有 min(ai’, aj’) >= min(ai, aj) 才行。

所以就可以采用头尾双指针往中间移动：

left = 0, right = n-1

  1. a[left] < a[right], left++
  2. a[left] > a[right], right–
  3. a[left] = a[right], left++, right–

终止条件：left >= right

我的代码：

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxArea(vector<int>& height) {
        int ans = 0;
        int l = 0, r = height.size() - 1;
        while(l < r){
            ans = max(ans, min(height[l], height[r]) * (r -l));
            height[l] < height[r] ? ++l : --r;
        }
        return ans;
    }
};

Runtime：20ms Memory：10.2MB