LeetCode--Longest Palindromic Substring

发表于 | 分类于 |

题目描述：

Given a string s, find the longest palindromic substring in s. You may assume that the maximum length of s is 1000.

样例：

1
2
3
Input: "babad"
Output: "bab"
Note: "aba" is also a valid answer.
1
2
Input: "cbbd"
Output: "bb"

就给泥萌看一个非常智障的蚊子，给泥萌看看蚊子的心路历程，嘤嘤嘤~

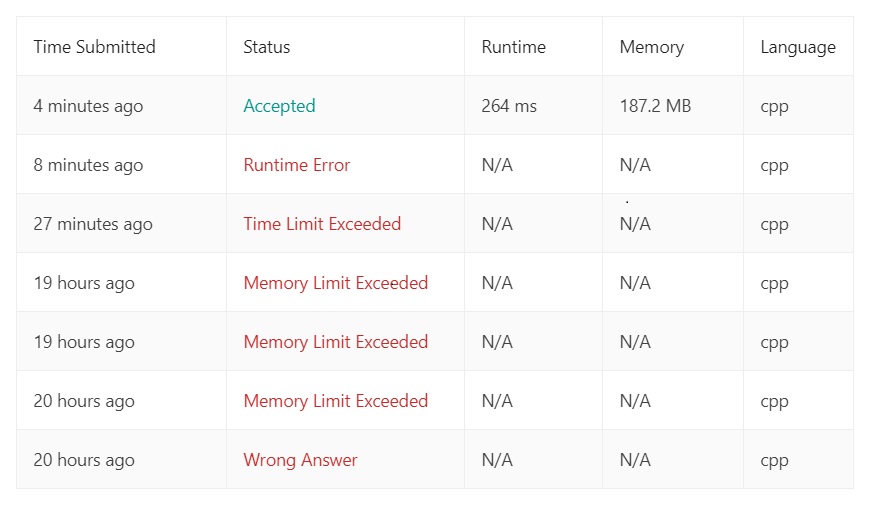
Longest Palindromic Substring

就为什么这么多爆空间呢？

当然是蚊子不想用 DP，然后就开始莽，就直接遍历每一次就使用 string 的字符串截取函数 substr()，来生成新的 string，然后又使用 reverse() 函数来反转字符串，最后来判断俩 string 是否相同，然后就爆空间辣！

思路：

正解是 DP，就 $dp[i][j]$，表示 i 到 j 之间的字符串是否为回文串，那么怎么判断 $dp[i][j]$ 是回文串呢？

首先我们要想到如果 $dp[i][j]​$ 是回文串，那么 $dp[i + 1][j - 1]​$ 一定是回文串，并且当 $s[i] == s[j]​$ 的时候，$dp[i][j]​$ 所表示的 i 到 j 之间的字符串就为回文串了，这样我们就有了：

$dp[i][j] = dp[i + 1][j - 1] \& (s[i] == s[j]) $

这一个 dp 状态方程；

那么接下来就是，每一个单个字符，肯定也是回文串，所以就有 $dp[i][i] = 1$，这样也就有了初始状态；

但是此时我们发现写出来的代码，第二个样例 “cbbd”，不能通过，这是为什么呢？

因为当 len = 2 的时候，它们中间没有 $dp[i + 1][j - 1]$，所以我们此时就要判断一下

最后的代码就如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    string longestPalindrome(string s) {
        if(s.size() == 0) return "";
        int n = s.size();
        vector<vector<int> > dp(n, vector<int>(n, 0));        
        int begin = n - 1;
        int len = 1;
        dp[n - 1][n - 1] = dp[0][0] = 1;
        for(int i = n - 2; i >= 0; --i){
            dp[i][i] = 1;
            for(int j = i + 1; j < n; ++j) {
                if(j == 0) continue;
                dp[i][j] = dp[i + 1][j - 1] & (s[i] == s[j]);
                if(j == i + 1 && s[i] == s[j]) dp[i][j] = 1;
                if(dp[i][j] == 1){
                    if(len < j - i + 1){
                        len = j - i + 1;
                        begin = i;
                    }
                }
            }       
        }
        return s.substr(begin, len);
    }
};

Runtime：264ms Memory：187.2MB